1

有一个借马分马的数学故事，想必大家都非常熟悉。

从前有一位阿拉伯的老牧人，在他临终时对着围在床前的三个儿子说：”我有十七匹马，留给你们，三个人分。分马的时候，老大呢，出力最多，得总数的二分之一；老二嘛，得总数的三分之一；老三最小，你呀，就拿总数的九分之一。但是不许把马杀死或者卖掉。”

勉强说完这几句，老牧人人就去世了。三兄弟执行遗嘱时，一致认为这些马是父亲生前心爱之物，决不能将其中任何一匹劈成几块瓜分，而且牧人是不许残害自己的朋友的（马）。但是遗嘱又要完全照办，如何是好呢？

这时一个智者骑着一匹马来了，并把自己的马借给了他们，这下总共就有18匹马，按照遗嘱的分法，老大分二分之一就是9匹，老二三分之一6匹，老三九分之一就是2匹马。

这样分完最后还剩下18-9-6-2=1，剩下最后一匹，这当然就是临时借用的那匹，依然物归原主。

虽然解决这个问题的方法，感觉有点投机取巧，但是有时候为了解决一个疑难问题，引入一个新的东西做为过渡，就像化学反应中的催化剂一样，能起到点石成金的效果。

2

在初中的平面几何，以及后来高中学习的立体几何中，老师教给我们的解题技巧，有一招叫做“添加虚拟线”，有时候能不能快速解出一道立体几何题目，关键就在于你能不能找到那条正确的虚拟线。

我当时在几何学方面成绩还可以，考试也经常得满分。不过那些年做过太多的题目，早已忘得个精光，只有初中快毕业时我在一本辅导书上看到的一道题目，令我印象非常深刻。

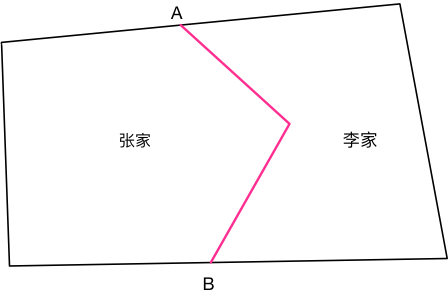
如下图，农民张家和李家有两块毗邻的田地，AB两点间的折线是两块田间的田埂，供行人行走。现在村民都觉得这段路是折线，走起来太远了，想要换成一条直线。那么你应该如何找出一条直线来重新分割两家人的田地，要求分割后各自家的田地面积必须与之前的一致，这样才公平。

意思就是要在A点和B点两边的直线上，分别再找两个点，然后把他们连接一条直接，按这条直接来重新修一个田埂。

这道题应该是中考的一个附加题目，我当时也想不出答案，看了参考答案之后，才觉得解法实在是精妙。

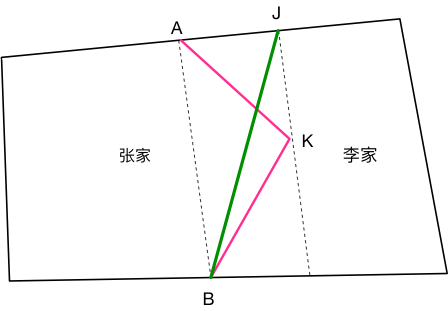
如下图所示，作虚拟线AB，然后经顶点K再做一条与AB线平行的虚拟线JK，连接线BJ就是满足要求的直线。

要证明其实很简单，因为AB与JK两条线平行，所以含有共同底边的两个三角形ABK与ABJ面积是相等的。

现在看起来这种题目无足挂齿，但作为成绩平平的中学生，我当时还是有一种眼前一亮的感觉。这种添加辅助线的解决思路，感觉威力无穷，实际上，也确实如此，很多数学家都是通过这种方法巧妙地解答了许多艰难的数学问题。

3

为了证明著名的数学公式勾股定理：a^2+b^2=c^2，众多数学家都使出了浑身解数，动用了比勾股定理本身还要高深很多的数学知识，来证明它。比如用行列式证明，用无穷级数证明，用高斯公式证明，等等…

而中国古代三国时期魏人刘徽，对勾股定理做出了绝妙的证明，没有用到任何高深的数学公式，这个方法被命名为“青朱出入图”而流传于世。

刘徽（公元3世纪）在注《九章算术》勾股术时说：“勾自乘为朱方，股自乘为青方，令出入相补，各从其类”。

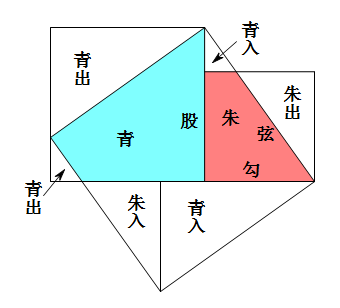
如上图，按直角三角形两条边“勾”、“股”，分别补出两个正方形，直角三角形的斜边同样也补出一个大的正方形，只要论证补出来的两个小正方形的面积，加起来等于大正方形面积，就可以证明勾股定理了。

三个正方形本来就有2块共同的区域（图中有颜色的部分），那么只要证明剩下的“青出”+“朱出”=“青入”+“朱入”就可以了。然而这一点显然是很容易做到的，小学生都可以，这里就不赘述了。

4

有这样一个被称为“缺损棋盘”的数学问题：我们有一张移走两个对角方块的棋盘，它只剩下62个方块。现在我们取31张多米诺骨牌，每一张骨牌恰好能覆盖住2个方块。

要问的是：是否可能将这31张多米诺骨牌摆得使它们覆盖住棋盘上的62个方块？

科学家将试图通过试验来解答这个问题，在试过几十种摆法后会发现都失败了。最终，科学家相信有足够的证据说棋盘不能被覆盖。然而，科学家永远也不能肯定确实是这种情形，因为可能有某种还没有试过的摆法却能获得成功。摆法有几百万种，只可能尝试其中的一小部分。

这时数学家登场了，数学家将通过逻辑论证来回答这个问题，这种论证将推导出无可怀疑地正确并且水远不会引起争议的结论。

棋盘上被移去的两个角都是白色的。于是现在有32个黑方块而只有30个白方块。

每块多米诺骨牌覆盖2个相邻的方块，而相邻方块的颜色总是不同的，即1块黑色和1块白色。

于是，不管如何摆骨牌，最先放在棋盘上的31张多米诺骨牌必定覆盖30个白色方块和30个黑色方块。

结果，总是留给你1张多米诺骨牌和2个剩下的黑色方块。

但是，请记住每张多米诺骨牌覆盖2个相邻的方块，而相邻方块的颜色是不同的。可是这2个剩下的方块颜色是相同的，所以它们不可能被剩下的1张多米诺骨牌覆盖。

于是，覆盖这棋盘是不可能的！

这个证明表明，多米诺骨牌的每一种可能的摆法都无法覆盖这个缺损的棋盘。

讲到这里，大家可能都还不清楚“棋盘问题”跟本文的主题“割补法”有什么关联。

我当时看到这个问题，多想了一步，假如，假如把题目做下小小的变化，移除棋盘是黑白颜色相间的这个前提条件，这个修改不会对题目本身造成影响。这时，你面对这个新的问题，棋盘64个全是白色的，缺失了对角的那两块，你将如何解决？

有了上面的解决思路，就好办多了，第一步把棋盘给染上黑白两色，然后再用上面的证明方法，不就可以了嘛？