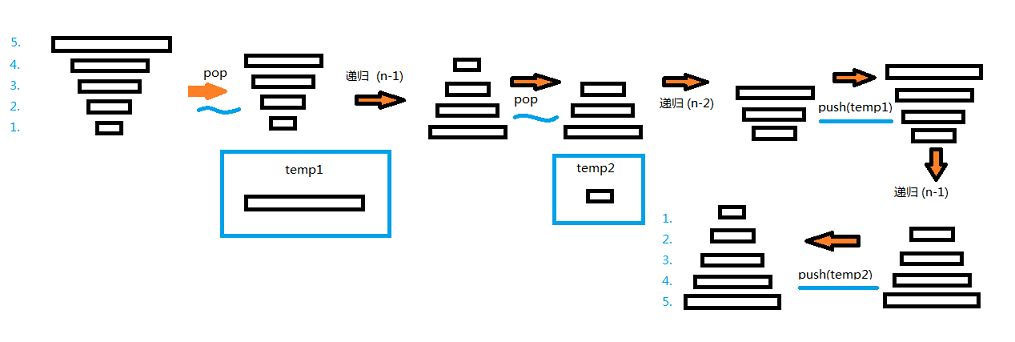
递归反转栈的顺序
要求只使用常数量个变量
我们要反转一个栈,如果使用另外一个栈作为辅助的话,那么反转起来很简单,一个接一个push到辅助栈里再push回来就行了。那么假如不能使用辅助栈,数组等空间为O(n)的数据结构,只使用O(1)的空间复杂度即只能有常数个变量,怎么实现将栈反转?即原来的栈顶在栈底,栈底变成栈顶。
解决办法如图示例
- 首先假设栈里面从栈底到栈顶存储的依次是 1 2 3 4 5,我们反转以后希望得到的结果是 5 4 3 2 1.
- 第一步pop出来第一个数5,存到temp1中,此时的栈中由下到上是1 2 3 4。
- 递归调用自身,不用考虑具体的过程,我们只需要知道这个递归调用结束后得到的结果是使栈中的元素变成了由下到上 4 3 2 1(因为这个函数本身的意思就是反转栈)。
- 此时pop出来第二个数1 ,存到temp2中,此时的栈中由下到上是 4 3 2。
- 再递归调用本身,抽象考虑这个递归完成后得到的结果是栈中的值变成了 2 3 4。
- 接着我们把push(temp1),栈变成了 2 3 4 5。
- 接着递归调用本身,递归完成后栈变成了 5 4 3 2。
- 接着push(temp2)。好了,栈变成了 5 4 3 2 1,反转完成!
- 接下来我们需要考虑递归函数结束的条件了,该函数的结束条件是当栈为空或者栈里只有一个元素的时候,return。
如何知道栈里只有一个元素?
我们可以先记录下栈顶元素,然后pop,如果栈变成空,则说明是只有一个元素,push回去再return。
def reverse_stack(stack):
if len(stack) == 0:
return
# 如果s里面只有一个元素,就返回,否则就不返回。具体实现是先pop出来一个,判断剩下的是不是空栈。
topa = stack.pop()
if len(stack) == 0:
stack.append(topa)
return
stack.append(topa)
temp1 = stack.pop()
reverse_stack(stack)
temp2 = stack.pop()
reverse_stack(stack)
stack.append(temp1)
reverse_stack(stack)
stack.append(temp2)
if __name__ == '__main__':
arr = [1, 3, 1, 4, 5, 3, 6, 2]
reverse_stack(arr)
assert arr == [2, 6, 3, 5, 4, 1, 3, 1]
支持获取最小值的栈
请设计一个栈,除pop与push方法,还支持min方法,可返回栈元素中的最小值。push、pop和min三个方法的时间复杂度必须为O(1)
这是LeetCode上面的一道题目,https://leetcode.com/problems/min-stack/description/
思路1:将每次入栈的元素及当前最小值一起存进去。
class MinStack(object):
def __init__(self):
self.stack = []
def push(self, x):
cur_min = self.getMin()
cur_min = cur_min if cur_min!=None else sys.maxint
self.stack.append((x, min(cur_min, x)))
def pop(self):
self.stack.pop()
def top(self):
if self.stack:
return self.stack[-1][0]
return None
def getMin(self):
if self.stack:
return self.stack[-1][1]
return None
思路2:可以利用额外的栈来记录最小值,这样可以节省空间。
import sys
class MinStack(object):
def __init__(self):
self.stack = []
self.mins = []
def _min(self):
if self.mins:
return self.mins[-1]
return sys.maxint
def push(self, x):
self.stack.append(x)
if x <= self._min():
self.mins.append(x)
def pop(self):
v = self.stack.pop()
if v == self._min():
self.mins.pop()
return v
def top(self):
if self.stack:
return self.stack[-1]
return None
def getMin(self):
return self._min()
按升序对栈进行排序
编写程序,按升序对栈进行排序(即最大元素位于栈顶)。最多只能使用一个额外的栈存放临时数据,但不得将元素复制到别的数据结构中(如数组)。该栈支持如下操作:push、pop、peek和isEmpty。
假设有如下两个栈,其中s2是“排序的”,s1则是未排序的:
s1 = [5, 10, 7] s2 = [12, 8, 3, 1]
从s1中弹出5时,我们需要在s2中找个合适的位置插入这个数。在这个例子中,正确位置是在s2元素3之上。怎样才能将5插入那个位置呢?我们可以先从s1中弹出5,将其存放在临时变量中。然后,将12和8移至s1(从s2中弹出这两个数,并将它们压入s1中),然后将5压入s2。
步骤1 s1 = [10, 7] s2 = [12, 8, 3, 1] tmp = 5 步骤2 s1 = [8, 12, 10, 7] s2 = [3, 1] tmp = 5 步骤3 s1 = [8, 12, 10, 7] s2 = [5, 3, 1] tmp = --
注意,8和12仍在s1中,这没关系!对于这两个数,我们可以像处理5那样重复相关步骤,每次弹出s1栈顶元素,将其放入s2中的合适位置。
def stack_sort(s):
s2 = []
while s:
tmp = s.pop()
while s2 and s2[-1] > tmp:
s.append(s2.pop())
s2.append(tmp)
return s2